Untuk mencari koefisien dari suatu persamaan yang berbentuk (x + y)nmemiliki beberapa cara yang sering digunakan. Salah satunya dengan cara menjabarkan persamaan tersebut kemudian menentukan koefesien yang ingin ditentukan.
(x + y)0 = 1
(x + y)1 = x + y
(x + y)2 = x2 + 2xy + y2
(x + y)3 = x3 + 3x2y + 3xy2 + y2
(x + y)4 = x4 + 4x3y + 6x2y2 + 4xy3 + y4
(x + y)5 = x5 + 5x4y + 10x3y2 + 10x2y3 + 5xy4 + y5
(x + y)6 = x6 + 6x5y + 15x4y2 + 20x3y3 + 15x2y4 + 15xy5 +y6
atau menggunakan segitiga pascal seperti dibawah ini.
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
Dari cara menjabarkan diatas, bisa diperumum lagi untuk mempermudah perhitungan suku dan koefesiennya. Aturan untuk menjabarkan bentuk perpangkatan (x + y)n adalah
- Suku pertama adalah xn, sedangkan suku terakhir adalah yn
- Pada setiap suku berikutnya, pangkat x berkurang satu sedangkan pangkat y bertambah satu. Untuk setiap suku, jumlah pangkat x dan y adalah n
- Koefesien untuk xn-kyk, yaitu suku-(k + 1), adalah C(n, k). Bilangan C(n, k) disebut koefesien binomial.
Dari aturan diatas dapat disimpulkan bahwa
(x + y)n = C(n, 0)xn + C(n, 1)xn-1y1 + … + C(n, k)xn-kyk + … + C(n, n-1)x1yn-1+ C(n, n)yn
= 
C(n, k)xn-kyk
C(n, k)xn-kyk
Aturan secara umum ini dinamakan Koefesien Binomial
Contoh :
Tentukan suku keempat dan koefesien dari (x – y)5
Cara I : penjabaran
(x – y)5 = (x + (-y))5
=
x5 + 5x4(-y) + 10x3(-y)2 + 10x2(-y)3 + 5x(-y)4 + (-y)5
x5 + 5x4(-y) + 10x3(-y)2 + 10x2(-y)3 + 5x(-y)4 + (-y)5
= x5 – 5x4y + 10x3y2 – 10x2y3 + 5xy4 – y5
Jadi suku keempatnya adalah -10x2y3 dan koefesienya adalah -10
Cara II : segitiga pascal
perhatikan baris keenam pada segitiga pascal diatas : 1 5 10 10 5 1. Sehingga suku keempatnya adalah 10x2(-y)3 = -10x2y3 dan koefesiennya = -10
Cara III : koefesien binomial
(x + (-y))5
C(n, k)xn-kyk
C(5, 3)x5-3(-y)3
= 
x2(-y)3
x2(-y)3
= 
x2(-y)3
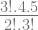x2(-y)3
= 10x2(-y)3
= -10x2y3
Jadi suku keempatnya adalah -10x2y3 dan koefesiennya adalah -10
Sumber :
Munir, R., 2009, Matematika Diskrit, Informatika, Bandung.
